Determine reactions at supports:

Determine reactions at supports of supported beam of 6m span carrying increasing load of 1500N/m to 4500N/m from one end to another end. 

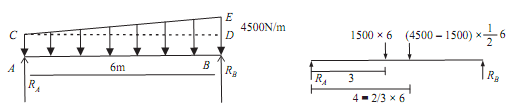
Sol.: As Beam is simply supported that is, at point A and point B only point load is acting. At first change UDL and UVL in point load. As shown in the given figure. Let ∑H & ∑V is the sum of horizontal and vertical component of Resultant forces, the supported beam is in equilibrium, therefore resultant force is zero.

Draw the free body diagram of the beam as shown in the given figure

Divided the diagram ACBE in to two parts A triangle CDE and a rectangle ABCE. Point load of Triangle CDE =1/2 × CD × DE = 1/2 × 6 × (4.5 -1.5)= 9KN

act at a distance 1/3 of CD (i.e., 2.0m )from point D

Point load of Rectangle ABCD = AB × AC = 6 × 1.5 = 9KN

act at a distance 1/2 of AB (i.e., 3m )from point B

Now apply condition of equilibrium:

∑H = 0;

R_AH = 0                                         .......ANS

∑V = 0;

R_A  -1500 × 6 - 3000 × 3 + R_B = 0

R_A  + R_B = 18000 N                                                                                   ...(i)

Now taking moment about 'A'

- R_B  × 6 + 9000 × 3 9000 × 4 = 0

R_B = 10500 Nm                       .......ANS

Putting the value of R_B  in the equation (i)

R_A = 7500 Nm                         .......ANS