Problem 1. Consider the demand function Q(p₁, p₂, y) = p₁^-2 p₂y₃, where Q is the demand for good 1, p₁ is the price of good 1, p₂ is the price of good 2 and y is the income. Suppose the current prices and income are (p₁, p₂, y) = (1, 2, 1).

(a) Find the current demand for good 1.

(b) Find the formulas for the partial derivatives of the demand function with respect to p₁, p₂, y.

(c) Evaluate the partial derivatives found in (b) at the current prices and income.

(d) Use the di?erentials to approximate the change in the demand as p1 increases by 0.1, p₂ decreases by 0.2 and y stays the same.

Problem 2. Estimate 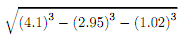  using differentials.

Problem 3. Consider the production function Q(x, y) = x² + y² + xy, where Q is the output, x is the quantity of input 1, y is the quantity of input 2. Suppose the current quantities of inputs are (x, y) = (5, 2).

(a) Find the current output.

(b) Find the formulas for the partial derivatives of the production with respect to x and y.

(c) Evaluate the partial derivatives found in (b) at the current quantities of inputs.

(d) Assume the ?rm is planning to retire one unit of input 1. Use the Implicit Function Theorem to estimate the corresponding change in quantity of input 2 that would keep the output at its current level.

Problem 4. One solution of the system x³y - z = 1, x + y² + z³ = 6 is (x, y, z) = (1, 2, 1). Estimate corresponding x and y when z = 1.1.