Determine acceleration of weight:

Two pulleys of radii 200 mm and 400 mm are mounted co-axially and rigidly on a common-shaft.

These pulleys have a overall mass of 28 kg and radius of gyration of 200 mm of the combination. If weights W₁ = 40 N and W₂ = 50 N are suspended from points A₁ and A₂ by ropes which are wound round the two pulleys, determine acceleration of weight W₂. Suppose g = 10 m/sec².

Solution

 Clockwise moment of W₁ about centre of pulley

= 40 × 0.4 = 16 N.m.

Anticlockwise moment of W2 about centre of pulley = 10 N.m.

Therefore the pulley shall rotate clockwise with angular acceleration α about the centre. After some time, W₂ shall have moved a distance s₂ with acceleration a₂ and shall have velocity of v₂  = r₂  ω , while W₁ will move

Distance  s₁ = 2 s₂  = 2 r₂  θ .

with final velocity V₁ = r₁  ω = 2 V₂

with acceleration .a₁ = r₁  α = 2 a₂

Since,   r_k  = 0.2 m.

I _(m) = 28 × (0.2)²       = 1.12 kg m²

ω² = 2 × α θ

By Using Principle of Conservation of Energy, and letting datum level as (A - A),

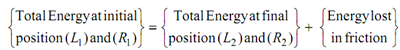
40 (s₁ ) + 50 (s_o) = 50 (s₁/2)  + 50 (s_o) + (40/10) × (V₁)² /2+ 50 × (V₂)² /2+( I_m ω² )/2

40 (s ) - 25 s = ω² [2  × (0.4)² + 2.5 × (0.2 )² +(1.12/2)]

15 × (0.4 θ) = 2 α θ [0.32 + 0.1 + 0.56]

∴ α = 3.06 rad / sec ²

α ≈ 3 rad / sec ² .