The Carnot cycle consists of four processes in succession:

1. isothermal compression from T_L, V₁ to T_L, V₂

2. adiabatic compression from T_L, V₂ to T_H, V₃

3. isothermal expansion from T_H, V₃ to T_H, V₄

4. adiabatic expansion from T_H, V₄ to T_L, V₁

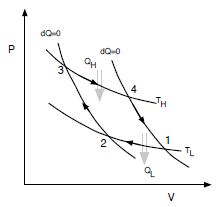
Analyze the cycle, assuming an ideal gas as working uid, by doing the following:

a) Compute the work done in each leg of the process.

b) Compute the total work done over the cycle. Is the work done on the system, or by the system?

c) Compute the heat flow QL during the isothermal compression from T_L, V₁ to T_L, V₂. Does the heat flow into the system, or out of the system?

d) Compute the heat flow QH during the isothermal expansion from TH, V3 to TH, V4. Does the heat flow into the system, or out of the system?

e) Verify that energy is conserved, i.e., that ΔU = W + QL + QH = 0 over the cycle.

f) Calculate the thermodynamic efficiency η , defined as  = -W=QH, the ratio of the work done by the system to the heat input. Express your answer in terms of TL and TH.