Demand Function is Homogeneous of Degree Zero:

Mathematical Presentation 

we will show that demand function is homogeneous of degree zero in prices and money income. In other words, if prices and money income change proportionately, then demand for all goods (and therefore the equilibrium bundle) remain the same. Initial price set p0 = (p10, p20,...,pn0) and the money income is I0 at which commodity vector x0 is bought, where x0 = (x10, x20,...,xn0) and p0x0 = I0. Let there be another commodity set x1 = (x11, x21,...,xn1).  At prices p0 set x1 is not chosen because it is not more expensive than x0 and at that price x1 is available so x0 is revealed preferred to x1. So,  

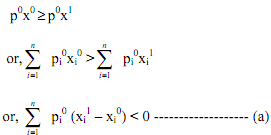
Consider a change in prices to p₁ = (p₁¹,...,p_n¹) and income changes to I₁, when consumer buys x₁. So x₀ at that new price level is not available to the consumer and we have,  

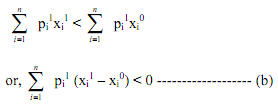
Let I¹ = m I⁰ and p¹ = m p⁰, where m is any positive number. Prices and income change in same proportion m and we have,  

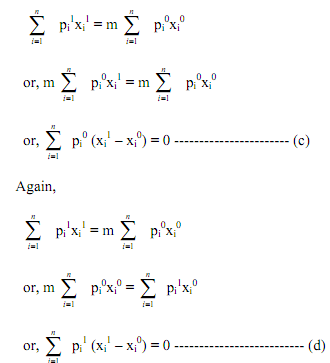
Equations (c) and (d) contradict equations (a) and (b). Hence, we conclude that the x¹ and x⁰ sets are identical and demand functions ( which are functions of prices and quantities) are homogeneous of degree zero and same proportional change in prices and income leads an individual to buy the same bundle.