Construction of an Isometric Projection - Transformation

In this projection, the direction of projection i.e. d = (d₁,d₂,d₃) makes an identical angles with all the 3-principal axes. Suppose here that the direction of projection d = (d₁,d₂,d₃) make equal angles as α with the positive side of the x,y, and z axes as in the Figure 13.

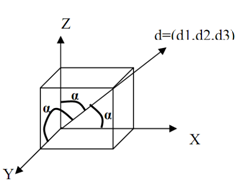
Subsequently

i.d=d₁=|i|.|d|.cosα  => cosα=d₁/|d|

Correspondingly

d₂=j.d=|j|.|d|.cosα  => cosα=d₂/|d|

d₃=k.d=|k|.|d|.cosα  => cosα=d₃/|d|

Consequently cosα=d₁/|d| = d₂/|d| = d₃/|d|

ð    d₁= d₂ = d₃   is actual

We select d₁=d₂=d₃=1

So here, we have d =(1, 1, 1)

Because, the projection, we are seeing for is an isometric projection => orthographic projection, that is, the plane of projection, must be perpendicular to d, hence d = n = (1,1,1). We suppose here that the plane of projection is passing via the origin.

ð  We identify the equation of a plane which is passing via reference point R(x₀,y₀,z₀) and consisting a normal

N = (n₁,n₂,n₃) is: (x - x₀).n₁ + (y - y₀).n₂ + (z -z₀).n₃=0

Because (n₁,n₂,n₃)=(1,1,1) and (x₀,y₀,z₀)=(0,0,0)

From equation (14), we have x + y + z = 0

Hence, we have the equation of the plane: x + y + z = 0 and d = (1,1,1)