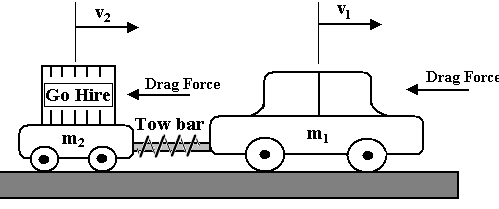
Consider a car of mass m1 is towing a trailer of mass m2 through a tow bar of stiffness k. Drag forces proportional to the car velocity (b1 v1) and the trailer velocity (b2 v2) are acting on the car and the trailer, respectively. The car engine provides enough traction force to do the towing task with a reasonable speed.

a) Differential equations describing the behaviour of the system,

b) State space representation of the system for the input traction force F, and the output position of the trailer,

c) Simulate the system using MATLAB and plot the response of the car and the trailer for a cycloidal force of 1000 N for duration of 1 minute.

d) Assume that the position of the car and the trailer can be detected by a GPS system. Design a state space controller based on Bessel transfer functions, and obtain the unit step response of the system.

e) Overall presentation.

Make necessary and reasonable assumptions if you think they are needed. Do not consider the friction between the tyres and the road.

t = 10 seconds , m1 = 1250 kg, m2 = 200 kg, k = 20,000 N /m

b1 = 40 kg / sec, b2 = 100 kg / sec