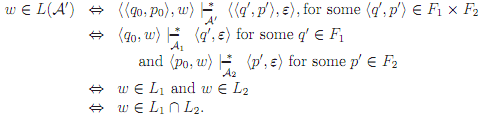Proof (sketch): Suppose L₁ and L₂ are recognizable. Then there are DFAs A₁ = (Q,Σ, T₁, q₀, F₁) and A₂ = (P,Σ, T₂, p₀, F₂) such that L₁ = L(A₁) and L₂ = L(A₂). We construct A′ such that L(A′ ) = L₁ ∩ L₂. The idea is to have A′ run A₁ and A₂ in parallel-keeping track of the state of both machines. It will accept a string, then, iff both machines reach an accepting state on that string.

Let A′ = (Q × P,Σ, T′ , (q₀, p₀), F₁ × F₂), where

T′ def= [{((q, pi, (q′, p′), σ) | (q, q′, σi)∈ T₁ and (p, p′, σ ∈ T₂}.

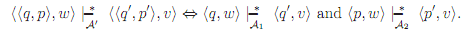
Then

(You should prove this; it is an easy induction on the structure of w.) It follows then that