Chi Square Test as a Test of Independence

In real life decision making, managers often have to know whether the differences between the proportions observed from a number of samples are serious enough to be probed further. In other words, a decision has to be taken whether these differences are significant enough to warrant setting up the hypothesis and testing it or whether they are due to chance. This is mandatory as it has a bearing on the future of the firm. We understand this further by taking an example. A brand manager of an FMCG wants to know whether the revenue from the sale of a product is uniform throughout the country or not. For this, he collects the data by conducting a survey consisting of 1000 consumers from each of the four zones. He arranges the data in rows and columns by classifying it in terms of the geographical location and whether the consumer purchases that particular brand or not. The significance level he chose was a = 10%. The data collected by him is as follows:

The table shown above is referred to as contingency table whose order is 2 x 4. That is, the table consists of two rows and four columns. We do not consider the row and the column under the head "total".

Setting up the Hypothesis

If the proportions of the total population of consumers in each of the four zones are denoted by p_N, p_w, p_S and p_E, then the null and the alternative hypothesis will be set up as follows:

H₀:    p_N = p_W = p_S = p_E        (Null hypothesis: Proportion of consumers from each of the four zones are equal)

H₁:    p_N  ≠ p_W   ≠  pS   ≠  pE    (Alternative Hypothesis: Proportion of consumers from each of the four zones are not equal)

If we accept the null hypothesis, the total proportion of the consumers buying the product can be calculated. In our example it is given by

=

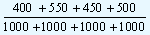1900/4000

= 0.475

Then the number of consumers who would not buy the product is 1 - 0.475 = 0.525. Using these two proportions, we can calculate the proportion of consumers who would either buy or not buy the product in each of the four zones. These figures give us the expected frequencies. They are shown in the table below.