Centre of Gravity and Moment of Inertia:

-  For a uniform plate of mass M, the overall mass may be divided into individual masses M_i for which centre of gravity is known as (x_i, y_i), the values of x, y for the centre of gravity of the overall mass is specified by

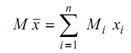
and

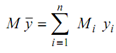
-  Distance of centroid of semicircular area of radius a through the centre is 4 a/3 π

-  Distance of centre of gravity of consistent wire bent into a shape of semicircular arc of radius a from its centre is equal to 2 a /π

-  Theorem I of Pappus and Guldinus

-  The area of the surface produced by revolving a plane curve around a non-intersecting axis in the plane of the curve is equal to the product of (a) length of the curve, and (b) the distance travelled through the centroid G of the curve throughout the revolution.

-  Theorem II of Pappus and Guldinus

-  The volume of solid produced by revolving a plane area A around a non-intersecting axis in its plane is equal to the product of (a) Area A, and (b) the length of the path travelled by the centroid G of the area throughout the revolution w.r.t. axis.

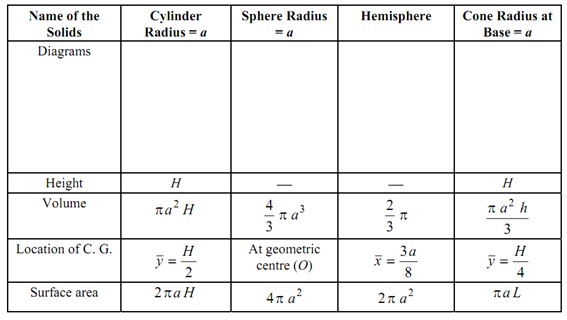
-  Particular parameters of some solids:

-  Area moment of inertia about x axis

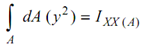
-  Area moment of inertia about y axis

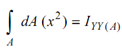
-  Parallel Axis Theorem : Area moment of inertia about X₁ X₁ axis at distance y₁ from XX = I _XX  +  A ( y₁ )²

-  Perpendicular Axis Theorem : If z axis is perpendicular to the plane of area A, then =  I _{z z}  = I _{x x}  +  I _{y y}