CENTRE OF GRAVITY:

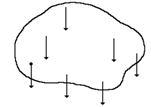
Consider a body as an accumulation of many small masses (molecules), all subject to gravitational attraction.  The total weight, which is a force, is equal to the sum of the individual masses, multiplied by the gravitational acceleration(g =9.81 m/s²).

          W  =  mg
The diagram shows that the individual forces all act in the same direction, but have different lines of action.

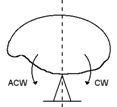
There must be datum position, such that the total moment to one side, causing a clockwise rotation, is balanced by a total moment, on the other side, which causes an anticlockwise rotation.  In other words, the total weight can be considered to act through that datum position (=  line of action).

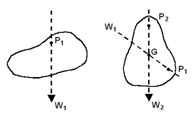
If the body is considered in two different position, the weight acts through two lines of action, W₁ and W₂ and these interact at point G, which is termed the Centre of Gravity.

Hence, the Centre of Gravity is the point through which the Total Mass of the body may be considered to act.

For a 3-dimensional body, the centre of gravity can be determined practically by several methods, such as by measuring and equating moments, and thus is done when calculating Weight and Balance of aircraft.

A 2-dimensional body (one of negligible thickness) is termed a lamina, which only has area (not volume).  The point G is then termed a Centroid.  If a lamina is suspended from point P, the centroid G will hang vertically below 'P₁'.  If suspended from P₂  G will hang below P₂.  Position G is at the intersection as shown.

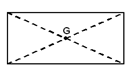
A regular lamina, such as a rectangle, has its centre of gravity at the intersection of the diagonals.

Other regular shapes have their centre of gravity at known positions, see the table below.

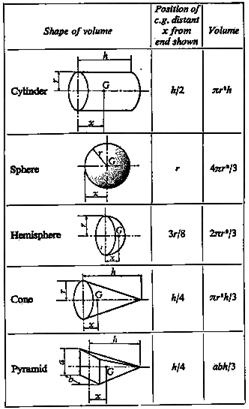
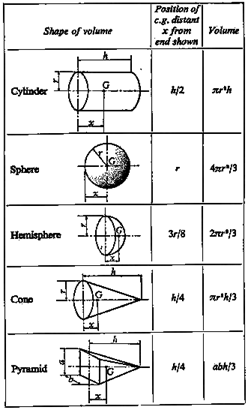
A triangle has its centre of gravity at the intersection of the medians.

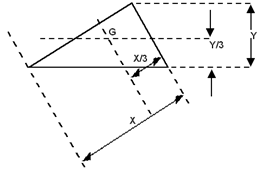
The centre of gravity can also be deduced as shown.

If the lamina is composed of a several regular shapes, the centre of gravity of that lamina can be deduced by splitting it into its regular sections, calculating the moments of these areas about a given datum, and then equating the sum of these moments to the moment of the composite lamina.

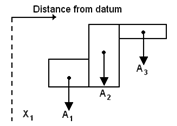
Expressed as an algebraic formula,

          A, X,  +  A₂ X₂  +  A₃ X₃  =  (A₁ + A₂ + A₃)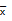

Where 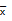 is the position of the centroid, with respect to the datum. This is the principle behind Weight and Balance.