This is a maple assignment, but it is also a research assignment. You will have to consult earlier worksheets, textbooks, and perhaps the internet to answer some of these questions - this is not only suggested, it is expected, so remember to reference your submission. Your submission does not have to be a .mws file, but if it is not it should be pdf.
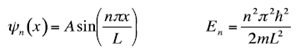
A Particle in a box
In order to answer the following questions you will need to consider an infinite potential well of length L, in which a particle has been confined.
1. For principal quantum number n=7, write code to calculate the normalization constant.
Then, plot the probability density function for this state (using L = 10).
2. Using the properly normalized wave equation from Question 1, write code to determine the expectation values <x> and 2> . Is one of the most probable positions? Explain why.
3. Using the properly normalized wave equation from Question 1, write code to determine the expectation values <p> and 2> . Show the value you obtain for 2> is equal to 2mE7 (where E7 is the energy of the n = 7 level). Remember that p is a differential operator so you will have to use the diff command.
4. The uncertainty of a quantum measurement is defined on page 222, Equation 6.41 (3rd edition SMM). Using this equation calculate the uncertainties of the position and momentum of a particle in the n = 5 state. Compute the product of these uncertainties and compare this with the prediction of the Heisenberg uncertainty principle.
Quantum oscillator
5. Repeat calculations in the previous question for the ground state wave function of the quantum oscillator. Comment on the obtained result.