Calculate the axial deflection and angle of rotation:

Any open coiled helical spring along with 10 complete turns is built of 16 mm diameter steel rod, the mean radius of the coil being 50 mm. The angle of helix is 28^o. Determine the deflection under an axial load of 300 N. Also determine the direct & shear stress induced in the section of the wire. If the axial load of 300 N is replaced by an axial moment of 9000 N-mm, calculate the axial deflection and angle of rotation.

Take E = 200 GPa, G = 80 GPa.

Also, determine the axial torque which shall cause a bending stress of 12 N/mm².

Solution

n = 10, d = 16 mm, R = 50 mm, α = 28o, W = 300 N

Δ= 64 W R³ n / d ⁴ cos α [cos² α/G + 2 sin ² α /E]

 = 64 × 300 × 50³ × 10 /16⁴ × cos 20 [cos2 20/80 × 10³ + 2 sin ² 20 /200 × 10³ ]

∴          Δ = 4.74 mm

σ_b  = 32 W R sin α / π d ³= 32 × 300 × 50 × sin 20 / (π × 16³) = 12.8 N/mm²

τ= 16 W R cos α/ π d ³ =16 × 300 × 50 × sin 20/ π × 16 =17.5 N/mm²

 Principal stresses,

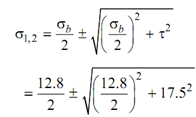
= 6.4 ± 18.6 = 25 N/mm² - 12.2 N/mm²

Maximum shear stress = (σ₁ - σ₂ ) /2= (25 - (- 1.22) )/ 2 = 18.6 N/mm²

M = 9000 N-m

φ= 64 M R n/ d 4 cos α [2 cos2 α/E    + sin 2 α / G]

=64 × 9000 × 50 × 10/(16)⁴ cos 20[(2 cos² 20)/ (200 × 10³)) +( (sin ² 20/ (80 × 10³))]

φ = 0.048 radians

φ= 64 M R² n sin α/ d ⁴[(1/G) -(2/E)]

= ((64 × 9000 × 50² × 10 × sin 20)/ (16)⁴ )[1/80 × 10³ - 2/200 × 10³]

= 0.19 mm

σ _b = 32 T cos α/ π d ³

⇒         12 = 32 T × cos 20 / π× 16³

∴ T = 5135.2 N-mm