The Null Hypothesis - H0:  There is no heteroscedasticity i.e. β₁ = 0

The Alternative Hypothesis - H1:  There is heteroscedasticity i.e. β₁ 0

Reject H0 if Q = ESS/2  >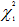

Regression Analysis: gt versus totexp, age, nk

The regression equation is

gt = 1.19 - 0.00208 totexp + 0.00002 age + 0.0111 nk

Predictor        Coef    SE Coef      T      P    VIF

Constant       1.1860     0.2229   5.32  0.000

totexp     -0.0020802  0.0009279  -2.24  0.025  1.045

age          0.000015   0.005019   0.00  0.998  1.038

nk            0.01105    0.07775   0.14  0.887  1.007

S = 1.46342   R-Sq = 0.3%   R-Sq(adj) = 0.1%

Analysis of Variance

Source            DF        SS     MS     F      P

Regression         3    11.167  3.722  1.74  0.157

Residual Error  1498  3208.095  2.142

  Lack of Fit    644  1373.116  2.132  0.99  0.540

  Pure Error     854  1834.980  2.149

Total           1501  3219.262

MTB > let k3=11.167/2

MTB > print k3

Data Display

K3    5.58350

Inverse Cumulative Distribution Function

Chi-Square with 3 DF

P( X <= x )        x

       0.95  7.81473

MTB > InvCDF .95;

Since Q = 5.58350 < 7.81 = 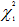, there is sufficient evidence to accept H0 which suggests that there is no heteroscedasticity from the Breusch-Pagan test at 5% significance level which means that one or more slopes are zero.