Biological Model

The most commonly used model of biological population is based on logistic growth model in which population is assumed to grow as a 'logistic curve' over time. In this model,  the population grows rapidly  in the early  stages as the abundance  of  food is more and  then the growth  rate slows down  and  then approaches asymptotically a level which is equal to its carrying capacity.

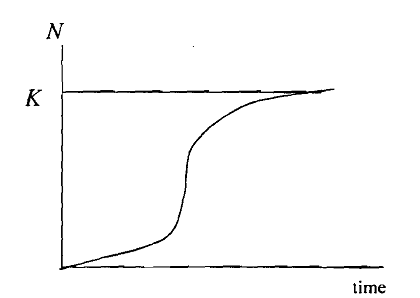
Diagram: Logistic Growth Curve

Observe that when plotted on graph the logistics curve is 'S' shaped and is given By

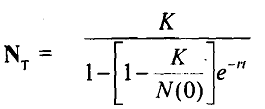
Where N_t is the number of organisms at a point of time t,

K is the carrying capacity, and

'r'  is maximum intrinsic per capita growth rate of population.

As the curve shows, the population initially increases at an  increasing rate and reaches a point at which the growth is maximum and after that, the growth is at a decreasing rate and then finally the growth stops when the population reaches the limit known as 'carrying capacity'. This indicates a limit of the stock, which is supported by a given habitat. By taking logarithm on both sides and differentiating, we obtain the growth rate.

By taking the logarithm of the logistic curve we obtain,

Equation 1

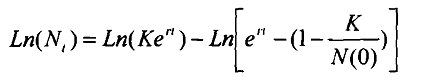
By differentiating the above we obtain

Equation 2

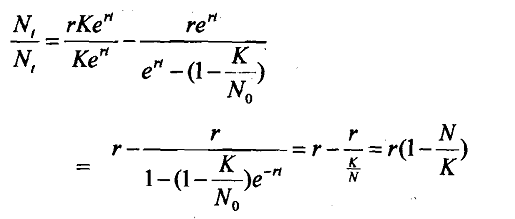
Here N_t is instantaneous rate of change of stock. When N approaches K, i.e., the carrying capacity, the effective per capita increase N_t/N_t declines linearly towards zero.

N_t= F (N) - h (t) where F (N) is natural growth rate.

The problem is to determine what pattern of harvest rates over time would cause the stocks to change in such a way as to maximize the value of yield it provides.