Question:

(a) Assume that a market is in equilibrium and all investors agree that the return on any diversified portfolio P is equal to

R_P = a_p + b_p1 F₁ + bp₂F₂ + · · · + b_pLF_L

What does the Arbitrage Pricing Theory says about the expected return of this portfolio?

(b)  Suppose that there are only 3 portfolios that are only available in the market and the following data are available.

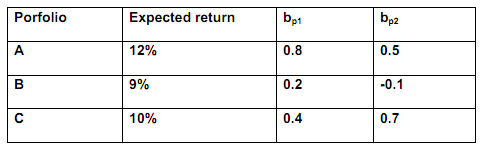
Based on the APT, if there are only two factors that influence returns, then the expected returns on any diversified portfolio P should satisfy the equation E[R_P] = λ₀ + bp₁λ₁ + bp₂λ₂ in equilibrium. Find the values of the factor prices.

(c) Consider a three-period binomial tree for the stock price.  Let S₀ = $210 and assume the stock price rises by 25% or falls by 20 at each time step.  Assume also  that the risk-free rate, r, is 5.12% per period.  A European call with strike price X =$70 expiring at time 3 is written on S.

(i) Find the probability measure which makes the discounted asset price a martingale?

(ii) Show that the price of the contingent claim is $60.371.

(iii) If the price movements for the asset were up-down-down, write down the trading strategy required to hedge the option.