APPLICATIONS OF NEWTON'S LAWS - II
1. As the body moves through the body it displaces the fluid. It has to exert a force on the fluid to push it out of the path. By the Newton's third law, the fluid pushes back on the body with an equal and opposite force. The direction of fluid resistance force on a body is always opposite to the direction of the body's velocity relative to the fluid.
The Newton's third law states that every action has equal and opposite reaction.
2. The magnitude of the fluid resistance force generally increases with the speed of the body through the fluid. Usually, f = kv (an empirical law). Suppose that you drop the ball bearing into a deep container filled with oil. After some time the ball bearing will approach its maximum (terminal) speed when the forces of gravity and friction balance each other:
mg = kv from which vfinal = mg / k.
3. The above was easy instance of the equilibrium under two forces. Generally, while solving the problems you should
a)draw a diagram,
b)define an origin for a system of coordinates,
c)identify all forces (tension, friction, normal, weight, etc) and their x and y components, d)Apply Newton's law separately along the x and y axes. e) find the accelerations, then velocities, then displacements. This sounds very easy task, and in fact it will happen to you naturally how to do this while solving the actual trouble.
4. Your weight in a lift: assume that you are in a lift which is at rest or is moving at constant velocity. In either case a=0 and the normal force N and the force due to gravity are exactly equal,
N - Mg = 0 ⇒ N = Mg. But if the lift is accelerating downwards then the Mg - N = Ma or N = M ( g - a) . Thus now the normal force (that is the force with which the floor of the lift is pushing on you) is decreased. Note that if the lift is accelerating or moving downwards with acceleration a then N=0 and you will experience weightlessness just like astronauts experience in space. Ultimately, if the lift is accelerating upwards then a becoms negative and you will feel heavier.
5. Suppose that you are in a railway wagon and want to know that how much you are accelerating. You are not able to look through the windows. A mass is hung from roof. Find the acceleration of car from the angle made by the mass.
6. Friction is a amusing kind of force. It does not make its mind which way to act until some other force compels it to make a decision. Assume a block lying on the floor. If you push it forward, friction will act backward. And if you push it to the left, friction will act to the hand side right. Or we can say that the direction of the frictional force is always in the opposite direction to the applied force.
7. Let us solve the given problem: a rope of the length L and mass per unit length m is placed on a table with a length l hanging from one edge. What should be l so that the rope just begins to slip?
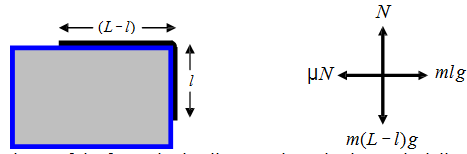
To solve this, look at the balance of the forces in the diagram given: in the vertical direction, the normal force balances the weight of the part of the rope the lies on the table:
N = m(L - l ) g. In horizontal direction, the rope exerts the force mlg to the right, which is counteracted by the friction that which to the left. Therefore μ N = mlg. Substituting N from the first equation we find out
l = μ L
 μ + 1
μ + 1
Note that if μ is very small in measure then even a small piece of string which hangs over the edge will cause entire string to slip down.