Analyse the beam:

Analyse the beam illustrated in Figure and draw the SFD, BND & thrust diagram. Situated the point of contraflexure, if any.

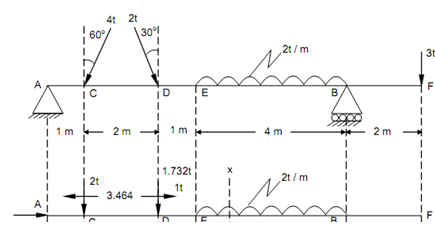
Figure

Solution

Vertical component of 4 kN at C, = 4 × cos 60^o = 2 kN ( ↓ )

Horizontal component of 4 kN at C, = 4 × sin 60^o = 3.464 kN ( ← )

Vertical component of 2 kN at D, = 2 × cos 30^o = 1.732 kN ( ↓ )

Horizontal component of 2 kN at D, = 2 × sin 30^o = 1 kN ( → )

Taking moment around A,

R _B   × 8 - (3 × 10) - 2 × 4 × (4 + (4/2)) - (1.732 × 3) - (2 × 1) = 0

R_B  = 10.6495 kN

R_A  = 2 + 1.732 + (2 × 4) + 3 - R_B  = 14.732 - 10.6495 = 4.0825 kN

Shear Force (beginning from the Left End A)

SF at A, F_A  = + 4.0825 kN

SF just left of C, F_C  = + 4.0825 kN

SF just right of C, F_C  = + 4.0825 - 2 = + 2.0825 kN

SF just left of D, F_D  = + 2.0825 kN

SF just right of D,  F_D  = + 2.0825 - 1.732 = + 0.3505 kN

SF at E, F_E  = + 0.3505 kN

SF just left of B, F_B  = + 0.3505 - (2 × 4) = - 7.6495 kN

SF just right of B, F_B  = - 7.6495 + 10.6495 = + 3 kN

SF just left of F, F_F  = + 3 kN = load at the end F.

Bending Moment (beginning from the F)

BM at F,          M_F   = 0

BM at B,  M _B  = - (3 × 2) = - 6 kN-m

BM at E, M _E  =+ (10.46 95 × 4) - (3 × 6) - ( 2 × 4 ×( 4/2))   =+ 8.599 kN-m

BM at D, BM at C,

M _D  = + (4.0825 × 3) - (2 × 2) = + 8.2475 kN-m

M _C  = + (4.0825 × 1) = + 4.0825 kN-m

 BM at A,        M_A = 0

Maximum Bending Moment

Maximum bending moment shall occur at B and among B and E. Consider a section XX at a distance x from the end F.

F_x  = - 10.6495 + 3 + 2 ( x - 2)

For maximum bending moment, F_x must be equal to zero.

- 10.6495 + 3 + 2x - 4 = 0

x = 5.82475 m ≈ 5.825 m

BM at section XX,

∴          M x = + 10.6495 ( x - 2) - 3x - 2 ( x - 2) × (( x - 2)/2)

                   = 10.6495 ( x - 2) - 3x - ( x - 2)²

M _max  = 10.6495 (5.825 - 2) - 3 (5.825) - (5.825 - 2)²

=+ 8.629 kN-m

Maximum positive bending moment = + 8.629 kN-m

Maximum negative bending moment = - 6 kN-m.

Point of Contraflexure

Equating the BM at section XX, to zero.

10.6495 ( x - 2) - 3x - ( x - 2)²  = 0

or         10.6495 x - 21.299 - 3x - x²  + 4 x - 4 = 0

or         x²  + 11.6495x - 25.299 = 0

or         x²  - 11.6495x + 25.299 = 0

Solving out by trial and error, we obtain x = 2.9 m.

Point of contraflexure is at a distance of 2.9 m from the end F.

Thrust Diagram

Horizontal reaction at A,

+ H _A  + 3.464 - 1 = 0

+ H _A  + 2.464 = 0

∴ H _A  =- 2.464 kN

 ('-' denote that the reaction is towards right)

The portion AC is subjected to a compressive force of 2.464 kN. The part CD is subjected to a tensile force of 1 kN (that means3.464 - 2.464 = 1).