This is at the heart of the analysis of electromagnetics. It is based on a series of experiments conducted by the French scientist Ampere (1775 - 1836), in which the force between two long, parallel wires was measured and related to the current flowing in each.He found that the force per metre length of wire was related to the current in each wire, I₁, I₂ and the distance apart, r, by:

F ∝ I₁.I₂/r

From which he concluded that all magnetic fields are produced by the flow of electric current. Subsequent investigations have shown this to be the case - even for permanent magnets due tothe motion of electrons in the atomic structure of the material

Ampere went on to develop his famous 'Ampere's Law'

If the magnetic field is integrated along a closed path, the result is equal to the current enclosedAmpere's law can then be expressed mathematically as

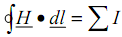
Where the dot product is used (= H.dl.cosθ) to indicatethat it is the magnetic field component resolved along the path direction at that point that is integrated. BothH and dl are vectors.

Although Ampere's Law applies to any closed path, it is convenient to choose a circular path, because the integration is then very easy.

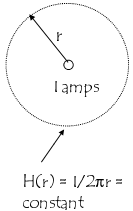
Thus;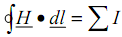

Becomes simply: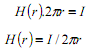

Note : If I is in amps and r in metres, then the units of H are Amps/metre

It is equally valid for an arbitrary path:

Arbitrary path enclosing a current carrying conductor. H(r) varies at different positions around the path

Direction of current is into the diagram. 

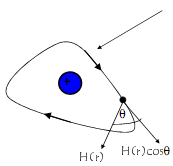
The direction of the magnetic field produced by the current is given by the 'right hand corkscrew rule'

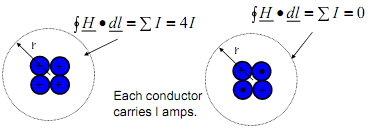
Note that Ampere's law applies to any closed path. If the path chosen does not enclose any current carrying conductors, then the result of the integration is zero.

Likewise, if more than one current carrying conductor is enclosed then the result of the integration will be the totalcurrent enclosed.