Acquire a transformation matrix for perspective projection for a specified object projected onto x=3 plane as viewed by (5,0,0).

Solution: Plane of projection: x = 3 as given. Here assume that P (x, y, z) be any point in the space. We identify the parametric equation of a line AB, beginning from A and passing   via B is like:

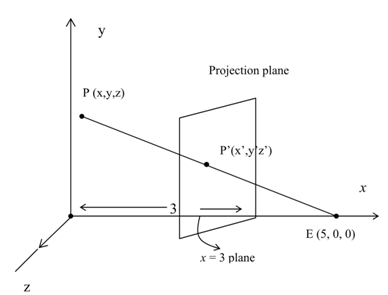
Figure: (i)

P (t) = A + t. (B - A), o < t < ∞

Consequently parametric equation of a line starting from E (5,0,0) and also passing via P (x, y, z) becomes:

E + t (P - E), o < t < ∞

=  (5, 0, 0) + t [(x, y, z) - (5, 0, 0)]

= (5, 0, 0) + [t (x - 5), t. y, t. z]

= [t. (x - 5) + 5, t. y, t. z].

Suppose here Point P' is obtained, as t = t*

∴ P' = (x', y', z') = [t* (x - 5) + 5, t*y, t*. z]

Because, P' lies on x = 3 plane, consequently

t* (x - 5) + 5 = 3 should be actual;

t* = -2/(x - 5)

P' = (x',y',z') = (3,((-2.z)/(x-5)), ((-2.z)/(x-5)))

= ((3x-15)/(x- 5), (-2y)/(x - 5), (-2z)/(x - 5))

In Homogeneous coordinate system there is:

P' = (x', y', z', 1) = ((3x-15)/(x- 5), (-2y)/(x - 5), (-2z)/(x - 5), 1)

= (3x - 15, - 2.y, - 2.z, x - 5)                  --------------(1)

In Matrix form it will be:

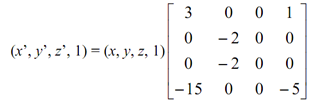
------------------------------(2)

Hence, as in above equation (2) is the needed transformation matrix for perspective view from (5, 0, 0).