Reference no: EM131140142

Consider the signal

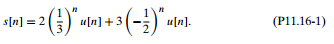
We wish to model this signal using a 2nd-order (p = 2) all-pole model or, equivalently, using 2nd-order linear prediction. For this problem, since we are given an analytical expression fors[n] and s[n] is the impulse response of an all-pole filter, we can obtain the linear prediction coefficients directly from the z-transform of s[n]. (You are asked to do this in part (a).) In practical situations, we are typically given data, i.e., a set of signal values, and not an analytical expression. In this case, even when the signal to be modeled is the impulse response of an all-pole filter, we need to perform some computation on the data, using methods such as those discussed in Section 11.3, to determine the linear prediction coefficients. There are also situations in which an analytical expression is available for the signal, but the signal is not the impulse response of an all-pole filter, and we would like to model it as such. In this case, we again need to carry out computations such as those discussed in Section 11.3.

(a) For s[n] as given in Eq. (P11.16-1), determine the linear prediction coefficients a1, a2 directly from the z-transform of s[n].

(b) Write the normal equations for p = 2 to obtain equations for a1, a2 in terms ofrss[m].

(c) Determine the values of rss[0], rss[1], and rss[2] for the signal s[n] given in Eq. (P11.16-1).

(d) Solve the system of equations from part (a) using the values you found in part (b) to obtain values for the aks

(e) Are the values of ak from part (c) what you would expect for this signal? Justify your answer clearly. (f) Suppose you wish to model the signal now with p = 3. Write the normal equations for this case.

(g) Find the value of rss[3]. (h) Solve for the values of ak when p = 3. (i) Are the values of ak found in part (h) what you would expect given s[n]? Justify your answer clearly. (j) Would the values of a1, a2 you found in (h) change if we model the signal with p = 4?