Reference no: EM131370836
A pharmaceutical company is planning to develop a new drug. The development will take place in two phases. Phase I will cost $1 million and Phase II will cost $2 million. Any new drug has to be approved by the FDA (U.S. Federal Drug Administration) before it can be marketed. If the drug is approved by the FDA, then a profit contribution of $6,250,000 can be realized by marketing the drug. The only fixed costs to be subtracted from this contribution is the $3 million development cost. In other words, if the drug is approved, the profit would be $3,250,000. If the drug is not approved, then all the development cost has to be written off as a loss. The managers estimate a 70% chance that the FDA will approve the drug. This still leaves a 30% chance of a $3 million loss. Because of the risk involved, one of the managers proposes a plan to conduct a test at the end of Phase I to determine the chances of FDA approval. The test itself will cost $165,000. If the test result is positive, the company will continue with Phase II; otherwise, the project will be aborted. The motivation for the test is that in case the chances of FDA approval are slim, at least Phase II costs can be saved by aborting the project. The manager has drawn the decision tree seen in Exhibit 1 to show possible outcomes. The tree shows the expenses and income along the relevant branches. However, the manager has not been able to arrive at the probabilities for the branches from chance nodes. The researcher who conducts the test says that the test is not 100% accurate in predicting whether the FDA will approve the drug. He estimates the following probabilities:

1. Given the above probabilities, compute the required probabilities for the decision tree. positive) and P (FDA will not approve | Test positive) for the case where the test is conducted. For the case where the test is not conducted, use the given non conditional P (FDA will approve) and P (FDA will not approve).]
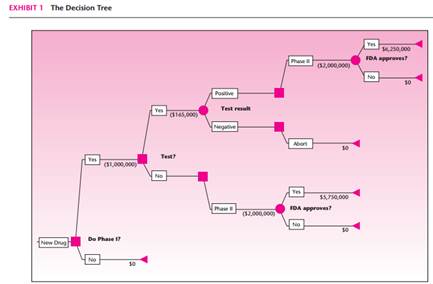
2. Assuming that the company wants to maximize the expected monetary value, what is the best decision strategy?
3. The company assumed that if the test result is negative, the best decision is to abort the project. Prove that it is the best decision.
4. At what cost of the test will the company be indifferent between conducting and not conducting the test?
5. Is your answer to question 4 the same as the EVSI of the test information?
|
One of my co-workers recently was laid off
: One of my co-workers recently was laid off, and then re-hired on a contract basis, and now she earns a lot less money doing the same job. I noticed that sometimes she takes home pads of paper and pencils, pens and other office supplies every once in ..
|
|
Probability that it will not crash at all in given semester
: What is the probability that it will crash at least two times in a given semester?- What is the probability that it will not crash at all in a given semester?
|
|
Calculate the expected time and variance for each activity
: You are responsible for managing an advertising and promotion project with the following activities (times are given in weeks). Using the PERT technique, calculate the Expected Time and Variance for each activity. What is the probability that the pro..
|
|
Why is patient advocacy important
: Discuss how these examples show how a person from an underserved population has limited access to healthcare. What would you do to help an underserved person access healthcare on a personal level, professional level and national level? Why is pati..
|
|
What is the best decision strategy
: The company assumed that if the test result is negative, the best decision is to abort the project. Prove that it is the best decision.
|
|
Was that the ethically correct choice
: Years ago in Seattle I worked for an insurance company with just one Jewish employee, who was a good friend of mine. He invented Jewish holidays, taking days off several times a year. As the only other employee at all familiar with Judaism, I could h..
|
|
How many calls a day should the squad be prepared for
: The squad wants to have at least 95% confidence of being able to handle all the calls received in a day. At least how many calls a day should the squad be prepared for?
|
|
What you think made your chosen entity go into bankruptcy
: Discuss what you think made your chosen entity go into bankruptcy, any significant measures it took during bankruptcy, and what happened to it once it came out of it.
|
|
Which approach to motivation is utilized in organization
: First, describe an organization that you are or were a part of (names not necessary, just a quick description for context). Then, state which approach to motivation is utilized in this organization, and explain how you know this
|