Reference no: EM13494
1. The current price of a bond is $114.72 and the current yield is 6.00%. The modified duration of the bond is 7.02. Use the modified duration to estimate the price of the bond if the yield increases to 6.10%.
A.114 B.120 C.210 D.220 E.300
2. A two-year bond has 8% annual coupons payable semiannually. The bond's yield is 10% compounded semiannually. Calculate the modified duration of the bond.
A.0.8 B.1.0 C.1.5 D.1.8 E.2.0 ok
3. A 22-year bond pays 7% annual coupons and has a current price of $81.12. The annual effective yield on the bond is 9%. The Macaulay duration of the bond is 10.774. Estimate the new price if the yield falls to 8.95%.
A.76 B.78 C.80 D.82 E.84
4. A 15-year mortgage is repaid with level monthly payments. The yield is 12% compounded monthly. Calculate the Macaulay duration of the mortgage.
A.3.2 B.5.4 C.7.1 D.9.7 E.10.3
5. A 20-year bond yielding 9% has a price of $127.79. If the bond's yield falls to 8.75%, then the price of the bond will increase to $130.65. If bond's yield increases to 9.25%, then the price of the bond will fall to $125.02. Calculate the effective duration of the bond.
A.8.6 B.8.7 C.8.8 D.8.9 E.9.0
6. A five-year bond with a coupon of 6.7% pays coupons semiannually. It is currently yielding 6.4%. Its current price is $101.2666. If the bond's yield increases by 10 basis points, then its price falls to $100.8422. If the bond's yield falls by 10 basis points, then its price rises to $101.6931. Calculate the effective convexity of the bond.
A.15.67 B.17.75 C.18.52 D.19.32 E.20.74
7. The modified duration of an 8-year bond is 5.35 and its convexity is 39.19. Estimate the percentage change in the price of the bond if its yield increases by 63 basis points.
A. -3.29% B.-1.09% C.1.09% D.3.29% E.5.14%
8. An insurance company has committed to make a payment of $100,000 in 5 years. The insurance company can fund this liability only through the purchase of 4-year zero-coupon bonds and 10-year zero-coupon bonds. The annual effective yield for all assets and liabilities is 12%. Determine how much the bank should invest in the 4-year zero-coupon bond in order to immunize its position.
A.26401 B.26933 C.47286 D.47813 E.48005
9. You are given the following information with respect to a callable bond:
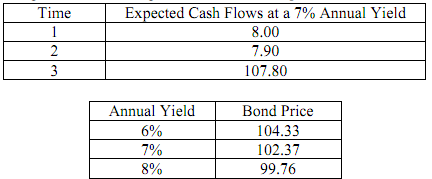
The current yield is 7%.
Calculate the ratio of the modified duration to the effective duration of this bond.
A.1.01 B.1.17 C.1.32 D.1.38 E.1.50
10. The current price of a bond is 100. The derivative of the price with respect to the yield to maturity is -700. The yield to maturity is 8%.
Calculate the Macaulay duration.
A.8 B.9 C.10 D.11 E.12
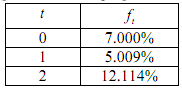
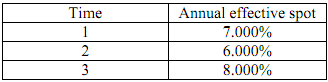
11. Given the following annual effective spot rates, find the present value of a 3-year bond paying 15% annual coupons and having a par value of $100.
12. Given the following yields and coupons for bonds with $100 of par value, determine the 2-year annual effective spot rate.
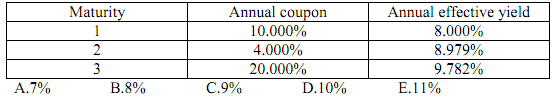
13. Given the following table of forward rates, find the present value of a 3-year bond paying 15% annual coupons and having a par value of $100.
A.118.66 B.120.24 C.132.86 D.144.12 E.151.97