Reference no: EM132136341

Assignment -

1. Let (T, ∧, ∨,', 0, 1) be a Boolean Algebra.

Define ∗ : T × T → T and o : T × T → T as follows:

x ∗ y := (x ∨ y)' x o y := (x ∧ y)'

(a) Show, using the laws of Boolean Algebra, how to define x ∗ y using only x, y, o and parentheses.

(b) Show, using the laws of Boolean Algebra, how to define x o y using only x, y, ∗ and parentheses.

Define R ⊆ T × T as follows: (x, y) ∈ R if, and only if, (x ∧ y) ∨ (x' ∧ y') = 1

(c) Show, using the laws of Boolean Algebra, that R is an equivalence relation. Hint: You may want to use the observation that if A = B = 1 then A ∧ B ∧ C = A ∧ B implies C = 1 (why?)

2. Let P F denote the set of well-formed propositional formulas made up of propositional variables, T, ⊥, and the connectives ¬, ∧, and ∨. Recall from Quiz 7 the definitions of dual and flip as functions from PF to PF:

dual(p) = p	flip(p) = ¬p
dual(T) = ⊥; dual(⊥) = T	flip(T) = T; flip(⊥) = ⊥
dual(¬φ) = ¬dual(φ)	flip(¬φ) = ¬flip(φ)
dual(φ ∧ ψ) = dual(φ) ∨ dual(ψ)	flip(φ ∧ ψ) = flip(φ) ∧ flip(ψ)
dual(φ ∨ ψ) = dual(φ) ∧ dual(ψ)	flip(φ ∨ ψ) = flip(φ) ∨ flip(ψ)

 (a) For the formula φ = p ∨ (q ∧ ¬r):

(i) What is dual(φ)?

(ii) What is flip(φ)?

(b) Prove that for all φ ∈ PF: flip(φ) is logically equivalent to ¬dual(φ).

3. Let P(n) be the proposition that: for all k, with 1 ≤ k ≤ n,

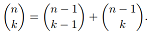
(a) Prove that P(n) holds for all n ≥ 1. (Note: it is possible to do this without using induction)

We can compute 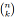from the formula given in lectures, however this can often require computing unnecessarily large numbers. For example,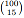= 253338471349988640 which can be expressed as a 64-bit integer, but 100! is larger than a 512-bit integer. We can, however, make use of the equation above to compute 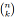more efficiently. Here are two algorithms for doing this:

Let trec(n, k) be the running time for chooseRec(n, k), and let t_iter(n) be the running time for chooseIter(n, k). Let T_rec(n) = max_0≤k≤n t_rec(n, k) and T_iter(n) = max_0≤k≤n t_iter(n, k) (so T_rec(n) ≥ t_rec(n, k) for all k, and likewise for T_iter(n)).

(b) Give an asymptotic upper bound for T_rec(n). Justify your answer.

(c) Give an asymptotic upper bound for T_iter(n). Justify your answer.