Reference no: EM13669445

1. Given the following directed graph,

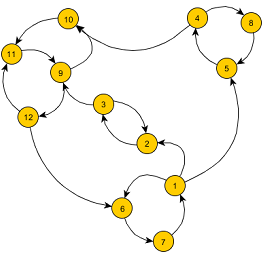
a. Find the number of strongly connected components in the graph,

b. Compute the in-degree centralization of the graph.

c. Find an edge in the graph that removal will results in the largest number of strongly connected components in the (residual/remaining) graph. Identify nodes in each strongly connected component after removing that edge.

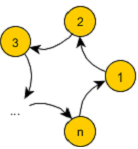
2. Consider a circular graph which consists of n vertices 1, 2., 3,...,n. There are directed edges from vertex i to i + 1 for i = 1, 2,..,n-1 as well as a directed edge from vertex n to vertex 1. Compute the (unnormalized) closeness centrality and the (unnormalized) betweenness centrality of each node in the graph.

3. Consider the random graph G(n, p), i.e. an Erdos-Renyi graph with n vertices and each edge exists with a probability p. Prove that the expected number of isolated nodes (nodes without any incident edges) is at most n(1 - p)^n-1.

4. Consider a graph G = (V, E) with the following adjacency matrix.

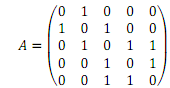
a. Identify an edge (u, v) with the highest edge betweenness centrality and compute its edge betweenness centrality.

b. If we remove the edge (u, v), identified in the 4b, what are the connected components in the graph (list the nodes in each component).

c. Compute the modularity matrix B in which B_ij = A_ij - k_ik_j/2m.

d. Consider the community structure in which each community is a connected component in 4b. Compute the modularity score associated with that community structure in G.

5. Consider an undirected graph G = (V, E) in which each edge (u, v) ∈ E exists with a probability 0 < p_uv ≤ 1. At the beginning of a diffusion process, the seed set S consists of exactly one node s ∈ V. For each node t ∈ V, denote by A(t) the probability that node t will be activated eventually with the seed set S = {s}. For example, A(s) = 1.

a. Prove that for any node w E V that have no path to s in G then A(w) = 0.

b. For a given edge (u, v) ∈ E, denote by

i. A_uv(t) the probability that node t will be activated eventually in case we remove the edge (u, v) from G, and

ii. A⁺_uv(t) the probability that node t will be activated eventually in case we merge two vertices It and v (that is to replace u and v with a new node r and connect r with all neighbors of u and v).

Prove that

A(t) = pA⁺_uv(t)+ (1 - p)A^-_uv(t)_.