Reference no: EM13854386

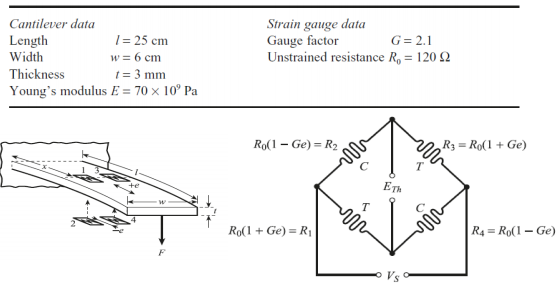
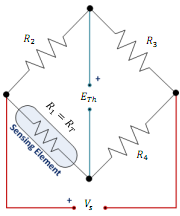
Question 1: Four strain gauges that are bonded onto a cantilever are connected to a resistive bridge as shown below. The strain is related to the applied force by: e = 6(l-x)/wt²EF. Given that the gauges are placed halfway along the cantilever and the cantilever is subject to a downward force of 0.5 N, use the data given below to calculate the resistance of each strain gauge and the bridge output voltage when V_s = 12 V.

Question 2: A variable dielectric capacitive displacement sensor consists of two square metal plates of side l = 5 cm, separated by a gap of d = 1 mm. A sheet of dielectric material 1 mm thick and of the same area as the plates can be slid between them as shown in below. Given that the dielectric constant (ε) of air is 1 and that of the dielectric material is 4:

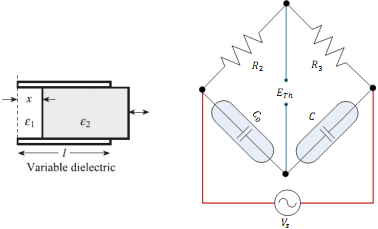
(a) Calculate the capacitance, C, of the sensor when the input displacement x = 0.0, 2.5 and 5.0 cm.

(b) The sensor is placed into a bridge as shown below. Given V_s = cos(400Πt) V, R₃/R₂= 1, and the bridge is balanced when c = c_min , find the output voltage, E_th, when the input displacement x = 2.5 and 5.0 cm.

Question 3: A capacitance level transducer is to be used to measure the depth h of liquid in a tank between 0 and 7m. The total length ??of the transducer is 8 m and the ratio b/a of the diameters of the concentric cylinders is 2.0. The dielectric constant ε of the liquid is 2.4 and the permittivity of free space ε₀ is 8.85pF/m. The transducer is incorporated into the deflection bridge as shown in figure R₂ = 100 Ω, R₃ = 10 kΩ and Vs = 15cos(400Πt)V.

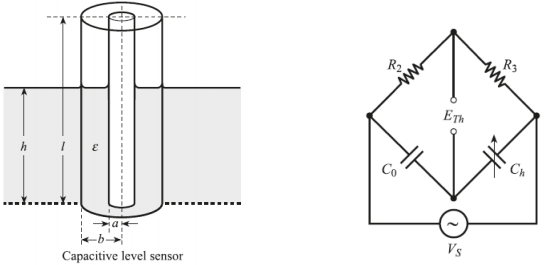
(a) Calculate the value of c₀ so that the amplitude E_Th is zero when the tank is empty.

(b) Using this value of c₀, calculate E_Th at maximum level.

(c) Explain why the relationship between E_Th and h is non-linear and calculate the nonlinearity at h = 3.5m as a percentage of full-scale.

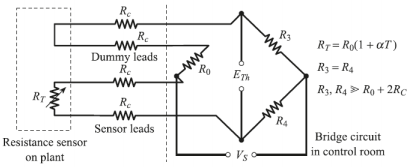
Question 4: The figure below shows a four-lead bridge circuit commonly found in oil & gas field instruments; Rc is the resistance of the leads or cables connecting the sensor to the bridge circuit. Show that E_Th = V_s(R₀/R₂)αT, i.e., the bridge output voltage is unaffected by changes in R_c.

Question 5: A platinum resistance sensor is to be used to measure temperatures between 0 and 200°C. Given that the resistance R_T in Ω as a function of the input temperature T°C is given by: R_T = R₀(1 + αT + βT² ) where R₀ = 100Ω, α= 3.91 × 10^-3 and β= -5.77 × 10^-7

 

(a) Find the maximum non-linearity as percentage of FS.

(b) A temperature sensor was inserted into a resistive bridge with DC excitation of Vs = 2.5 Vs as shown in the figure below.

i. Assuming the maximum allowed current is through the sensor 1 mA, what would be the value of R₄ such that the bridge is balanced when the input temperature is zero?

Approximate the result to the next higher standard resistance value.

ii. Find the resistance ratio R₃/R₂ and express the output voltage E_Th as a function of R_T

iii. Plot the bridge output voltage E_Th versus the input temperature T over the specified input temperature range.

Estimate the maximum non-linearity in the bridge output as percentage of output voltage and compare it to the value you found in (a).

(c) An instrumentation amplifier with parameters given in the table was used to amplifier the bridge output voltage.

i. Determine the required gain and value of the gain setting resistor R_G such that the G maximum voltage at the amplifier is 2.5V.

ii. Calculate the SNR when the input temperature is 100 °C. Assume R₃ = 2.4kΩ and 3 the amplifier noise equivalent bandwidth equals to the amplifier's 3dB bandwidth.

Question 6: Consider the measurement chain of Problem (5) consisting of the temperature sensor, bridge and instrumentation amplifier.

However, the bridge is now excited with AC sinusoidal voltage of frequency 1kHz such that Vs = 2.5cos(2 × 10³Πt).

(a) Write an expression for the voltage at the output of the amplifier when the input temperature is 100 °C. (assume the gain of the amplifier at f = 1 kHz equals to its DC gain determined in Problem (5).

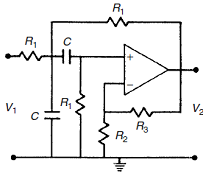
(b) The active bandpass filter shown in the figure was used to filter the signal at the output of the instrumentation amplifier (i.e., v₁ is the output of the in-amp).

i. Determine the values of R₁, R₂, R₃ and c such that filter is centered at 1kHz and provides a gain of 2.

ii. Calculate the SNR at the output of the filter and compare it to the value found in Problem (5).c.ii above. Ignore the noise generated in the filter's op-amp. Assume the filter noise equivalent bandwidth equals to the filter's 3dB bandwidth.