Inverse DFT using the FFT algorithm

The inverse DFT of the N-point sequence {X(k), k = 1, 2, ... , (N-1)} can be defined as

,   

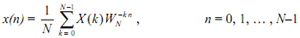here 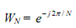. Take complex conjugate of x(n) and multiply by N to obtain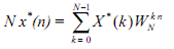 

The right hand side of above equation is simply DFT of the sequence X*

(k) and can be calculated by using any FFT algorithm. The output sequence which is desired is then found by taking the conjugate of result and dividing by N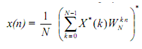   


Example Given DFT sequence X(k) = {0, (-1-j), j, (2+j), 0, (2-j), -j, (-1+j)} obtain the IDFT x(n) by using the DIF FFT algorithm.

Solution

This is an 8 point IDFT. The 8 point twiddle factors are, as computed earlier,

 
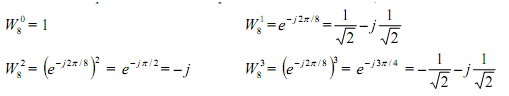
The elementary computation (Butterfly) is shown as follows:

 

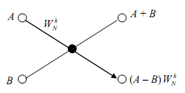
The signal flow graph id drawn as follows:
 

 

 

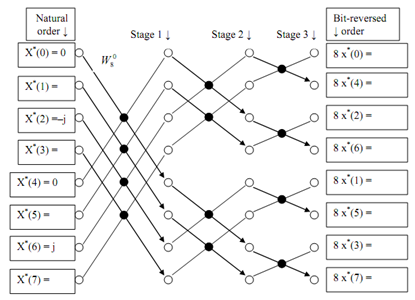
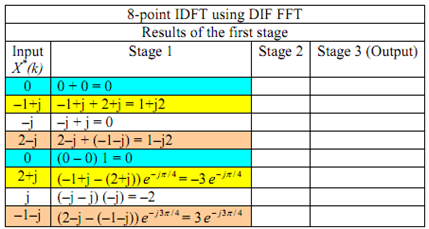
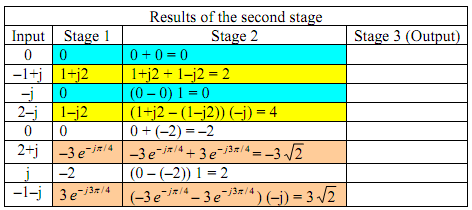
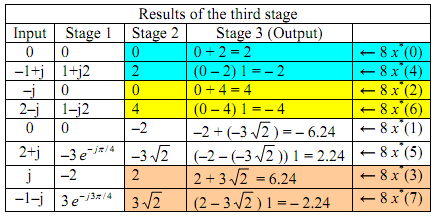
The output at the stage 3 gives us values in bit-reversed order:

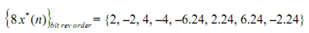
The IDFT can be given by arranging the data in normal order, taking complex conjugate of the

sequence and dividing it by 8:

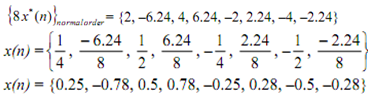
Because of the conjugate symmetry of {X(k)}, we should expect sequence {x(n)} to be

real-valued.

The MATLAB program:
 

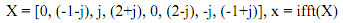
Example 3.4.2 Given DFT sequence X(k) = {0, (1-j), j, (2+j), 0, (2-j), (-1+j), -j}

obtain IDFT x(n) using the DIF FFT algorithm.

Solution
There exists no conjugate symmetry in {X(k)}. By using MATLAB

 

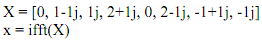
The IDFT is
x(n) = {0.5, (-0.44 + 0.037i), (0.375 - 0.125i), (0.088 + 0.14i), (-0.75 + 0.5i),

(0.44 + 0.21i), (-0.125 - 0.375i), (-0.088 - 0.39i)}

Email based Inverse DFT using the FFT algorithm assignment help - Inverse DFT using the FFT algorithm homework help at Expertsmind

Are you finding answers for Inverse DFT using the FFT algorithm based questions? Ask Inverse DFT using the FFT algorithm questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Inverse DFT using the FFT algorithm assignment help -Inverse DFT using the FFT algorithm homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours