Electromagnetism - Uniform Magnetic Field

Uniform Magnetic Field

Suppose a particle of mass m and charge q entering a uniform magnetic field induction B at O. with velocity making an angle θ with the direction of magnetic field acting in the pave of paper 

Resolving 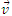   into two rectangular components we have. 

V cos θ = ( v₁) acts in the direction of the magnetic field and v sin θ = (v₂) acts pretend collar to the direction of magnetic field. For component velocity v₂ the force acting on the charged particle due to magnetic field is 

F‾ = q ( 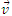 ₂ x   )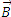

Or F‾ = q | 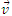  ₂ x 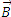  | = q v₂ B sin 90° = q (v sinθ) B

The direction of this force  F‾ is perpendicular to the plane consigning B and v₂ and hence acts perpendicular to the plane of the paper. As this force is to remain always perpendicular to v it cannot charge the magnitude of velocity v it charges only the direction of motion. Hence the charged particle is made to move on a circular path in the magnetic field. As shown in the force F on the charged particle due to magnetic field provides the required centripetal force (=mv22/r) necessary for motion along the circular path of radius r. 

∴ Bq v2 = m v2 2/r or v2 = B qr/m

Or v sin θ = B qr/m

The angular velocity of rotation of the particle in magnetic field will be 

W = v sin θ / r = B qr / mr = B q / m 

The frequency of rotation of the particle in magnetic field will be 

V = w / 2 π = Bq / 2 πm 

The time period of revolution of the particle in the magnetic field will be 

T = 1 / v = 2 πm / Bq

From (3) and (4) we note that v and T do not depend upon velocity of the particle. It means all the charged particles having the same specific charge (charge/mass) but moving with different paths due to component velocities perpendicular to the magnetic fields in the same time.

For component velocity v1 (=v cos θ), there will be no force on the charged particle in the magnetic field because the angle between v1 and B is zero thus the charged particle covers the linear distance in direction of the magnetic field with a constant speed v cos θ.

Therefore under the combined effect of the two component velocities the charged particle in magnetic field will cover linear path as well as circular path the path of the charged particle will be helical whose axis is parallel to the direction of magnetic field

The linear distance covered by the charged particle in the magnetic field in time equal to one revaluation of its circular path (known as pitch of helix) will be d = v₁ T = v cos θ² πm / Bq

Note:
 
If a charged particle having charge q is at rest in a magnetic field 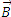   it experiences no force; as v = 0 and F = q v B sin θ.

If charged particle is moving parallel to the direction of 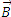 , it also does not experience any force because angle θ between  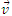  and 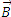     is 0 or 180° and particle in this situation will continue moving along the same path with the same velocity.

If charged particle is moving perpendicular to the direction of 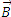   it experiences a maximum force which acts perpendicular to the direction of  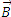  as well as  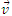 . hence this force will provide the required centripetal force and the charged particle will describe a circular pithy in the magnetic field of radius r given by mv2/r = Bq v.


ExpertsMind.com - Uniform Magnetic Field Assignment Help, Uniform Magnetic Field Homework Help, Uniform Magnetic Field Assignment Tutors, Uniform Magnetic Field Solutions, Uniform Magnetic Field Answers, Electromagnetism Assignment Tutors