Measures of Central Tendency
Average or measure of central tendency is a single quantity which enables us to know the average character of the data under investigation.
The following are the five measures of central tendency which are commonly used:
(i) Arithmetic mean (or simply mean average)
(ii) Median
(iii) Mode
(iv) Geometric mean
(v) Harmonic mean.
Arithmetic mean: It is the sum of the values of all observations in a series divided by the number of items constituting the series and is usually denoted by x.
Thus, if x1, x2, ... xn be the given n observations, 'then
¯x = (x1+x2 + …….+xn)/n = (∑_(i=1)^n¦x_1 )/n=(∑¦x)/n ,
where L denotes the sum of n items.
Theorem: If ¯x is the mean of observations x1, x2, x3, ………xn, then n
∑n(i=1)^n¦?(x_1-¯x)=0.?
Sum of the deviations of n observations from their mean is = 0.
If x is the mean of x1, x2, x3, xn; then the mean of
x1, + a, x2 + a, x3 + a1, ... + xn + a is ¯x + a
If ¯x is the mean of x1, x2, ... xn, then the mean of x1 - a, x2, - a, …..xn-a is ¯x -a
If ¯x is the mean of x1, x2, x3, ... xn, then the mean of ax1, ax3, ax3, …. axn is ¯ax where a ? 0.
Mean of grouped data: Let x1, x2, x3, ....... xn be n observations of the variate x with their frequencies f1, f2, f3, ... fn, respectively.
Then their mean ¯x is defined as
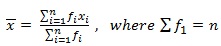
Mean for a grouped frequency distribution:
Find the class mark or mid¬-value xi of each class, as
xi = class mark
= ((lower limit + upper linit)/2)
Then, the formula, ¯x = (∑¦?fi xi)/(∑¦fi )
Short-cut method: From the given data, we suitably choose a term, usually the middle term and call it the assumed mean, to be denoted by A. We find the deviation, di = (xi - A) for each term. Then
Mean = A= (∑¦?fi di )/(∑¦fi )
Step-deviation method: When the width of classes are the same, then the following formula can-be used
Mean = x = A+h (∑¦?fi ui )/(∑¦fi )
where ui = (xi-A)/h and h is the width of each class.
Weight Arithmetic mean: While calculating a simple arithmetic mean, it was assumed that all items of the data were of equal importance. When these are not of equal importance, weights are assigned to them in proportion to their relative importance. If w1, w2, ... wn denote the weights (i.e., importance) given to the variates x1, x2 ... xn respectively, then the weighted arithmetic mean is given by
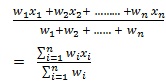
Mean of combined sets of data: If M and M be the two means computed or 'n and rf observations respectively, the mean M of (n1 + n2) observations of two groups taken together is given by
M= (n1 M1+ n2 M2)/(n1+n2 )
Replacement theorem: Let x1, x2, x3, ....... xn be n observations with mean ¯x if any observation, say xn is replaced by x’n, then the new mean is given by ¯x+(x_( n )^'-x_n)/n
Median: If the values of the data are arranged in ascending or descending order, then the median is the central value of the data. Thus median divides the total frequency into two equal parts.
Median of an ungrouped data: For the computation of median, it is necessary that the observations be arranged in ascending (or descending) order.
Median is the value of ((n+1)/2) th observation, when n is odd.

Median is the mean of the values of (n/2) th and (n/2+1) th observations, when n is even.
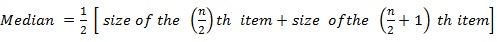
Median of Discrete series: First arrange the terms in ascending or descending order, then prepare a cumulative frequency table. Let the total frequency be n,
(i) If n is odd, then
Median = Size of the ((n+1)/2) th term.
(ii) If n is even, then
Median = 1/2 [ size of the (n/2)th item+size ofthe (n/2+1) th item]
Median in case of continuous frequency distribution:
(i) Prepare less than cumulative frequency (c.f.) distribution.
(ii) Find N/2.
(iii) Find the c.f. just greater than N/2.
(iv) The corresponding class contains the median value and is called the median class.
(v) The value of median is obtained by the formula.
Median = l+ h/f (N/2-C)
where l is the lower limit of the median class,
f is the frequency of the median class, c is the c.f. of the class preceding the median class and N = ∑¦f.
Alternative (By the use of ogive):
(i) Draw a cumulative frequency curve (ogive).
(ii) If there be n terms in the given distribution then use the ogive to (n/2) th or ((n+1)/2) th term which is the median of the given distribution, depending whether n is even or odd.
Quartiles: Quartiles are those values of the variate which divide the total frequency in four equal parts.
The lower Quartile (Q1) is mid-way between the lower extreme and the median.
The Upper Quartile (Q3) is mid-way between the median and the upper extreme.
The Middle Quartile (Q2) is the same as the median.
For Individual and Discrete Series:
Q1 = value of i ((n+1)/4) th item, where i = 1, 2, 3.
For continuous Series:
Qi = value of i (n/4) th item, where i = 1, 2, 3.
For Grouped Data:
Qi = l+ h/f (iN/4-C), i=1,2,3.
where l = the lower limit of the class in which the required particular value lies
f = the frequency of this class
h = the width of the class in which the partition value lies
N = ∑¦f
C = the c.f. of the class preceding the class in which the partition values lie.
Semi-inter quartile range
=1/2 (Q3-Q1 )=1/2 (25.5-15.5)
=1/2 (10)=5
Interquartile range: The difference between the upper quartile Q3 and the lower quartile Q1, is called inter quartile ¬range
i.e., Interquartile-range = Q3 – Q1, and Semi-interquartile range
= 1/2 (Q3-Q1 )
Mode: Mode is the value which occurs most frequently in a set of observations. It is paint of maximum frequency.
Live Math Experts: Help with Measures of Central Tendency Assignments - Homework
Expertsmind.com offers help with Measures of Central Tendency assignment and homework in mathematics subject. Experts mind’s math experts are highly qualified and experienced and they can solve your complex Measures of Central Tendency math problems within quick time. We offer email based assignment help –homework help service in all math topics including Measures of Central Tendency .
Math Online Tutoring: Measures of Central Tendency
We at Expertsmind.com arrange instant online tutoring session in Measures of Central Tendency math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Measures of Central Tendency Math topic and provide you tricky approach to solve complex Measures of Central Tendency problems.