Construction
Construction: To construct perpendicular bisector of a given line segment.
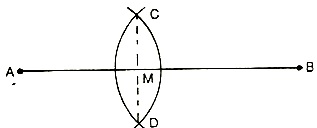
Steps of Construction:
1. With A as centre and radius greater than 1/2 AB, draw two arcs, one on either side of line AB.
2. With centre B, and the same radius (as in step 1), draw two arcs, intersecting the arcs of step 1 at C and D.
3. Draw the line CD. Line CD is the required perpendicular bisector of AB.
Construction: To construct a line perpendicular to a given line at a point on it.
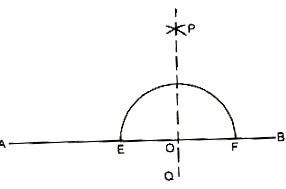
Steps of Construction:
1. With centre O and any radius draw an arc, intersecting AB in E and F.
2. With centres E and F and the same radius, draw arcs, on the same side of AB, intersecting each other in P.
3. Join PO and extend to line PO. PO is perpendicular to AB at O.
Construction: To construct a line perpendicular to a given line, from a point outside the line.

Steps of Construction:
1. With centre P and a radius of suitable length draw an arc intersecting AB in two points Q and R.
2. With centre Q and R and same radius greater than 1/2 QR, draw arcs on the same side of AB opposite to P, intersecting in S.
3. Join PS intersecting AB in N and produce to line PS. Line PS is the required line, perpendicular to AB.
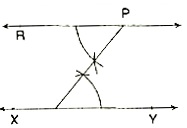
Construction: To construct the bisector of a given angle.
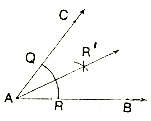
Steps of Construction:
1. With centre A and any radius draw an arc intersecting arms AB and AC in P and Q respectively.
2. With P, Q as centres, and radius greater than PQ, draw two arcs intersecting each other at R’
3. Draw the ray AR.'
The ray AR' is the requred bisector of ?BAC.
Construction: To construct an angle equal to a given angle.
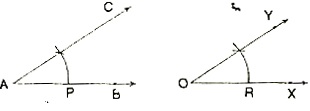
Steps of Construction:
1. With centre A and any radius draw an arc, intersecting arms AB and AC in P and Q respectively.
2. With centre Q and the sawn radius (as in step 1) draw an arc intersecting ray OX in R.
3. With centre R and radius PQ, draw an arc, intersecting the arc of step 2 in S.
4. Draw the ray OS and rename it OY OY is the required ray such that ?XOY = ?BAC.
Construction: To construct an angle of measure 60°, 120° and 130°.
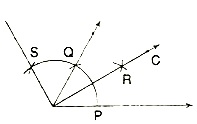
Steps of Construction:
1. With centre O and any radius, draw an arc, intersecting OX in P.
2. With centre P and same radius, draw another arc intersecting the first arc at Q.
3. Join OQ and produce it to ray OY Then ?XOY is the required angle of measure 60°.
4. With centre P and any radius, draw an arc, opposite to O.
5. With centre Q and same radius (as' in step 4), draw an arc, intersecting the arc in step 4 at R.
6. Join OR and produce it to ray OC.
Hence ?XOC is the required angle of measure 30°.
7. With the centre Q and same radius cut the arc at S.
8. Join OS and produce it to ray OD.
Hence, ?XOD is the required angle of measure 120°.
Construction: To construct angle of measure 90°, 45° and 135°.
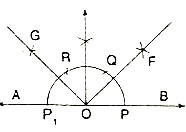
Steps of Construction:
1. Draw AB and take any point O on it.
2. With centre O and any radius, draw an arc, intersecting AB in P and P t
3. With centre P and same radius, draw another arc, intersecting the first arc at Q.
4. With centre Q and same radius, draw another arc, intersecting the first arc at R.
5. With centres Q and R and suitable equal radii, draw arcs, intersecting in S.
6. Join OS and produce it to ray AC.
7. Draw OF to bisect ?BOC, so that ?BOF = 45°.
8. Draw OG to bisect ?AOC, so that ?BOG = 135°.
Thus, ?BOC is the required angle of measure 90°.
Construction: To construct angles of measure 75° and 105°.
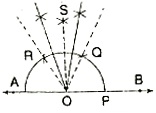
Steps of Construction:
1. Draw AB and take any point o on it.
2. Make ?BOQ = 60°, ?BOS = 90° and ?BOR = 120°.
3. Bisect ?QOS by OC, then ?BOC = 75°.
4. Bisect ?SOR by OD, then ?BOD = 105°.
Construction: Use properties of a rectangle, to draw a line parallel to a given line, at a distance 'h' from it.
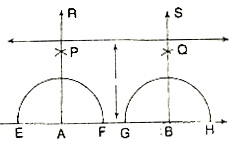
Steps of Construction:
1. Draw any line AB.
2. With centre A and any radius, draw an arc intersecting AB in E and F.
3. With centres E and F and the same radius, draw arcs on the same side of AB, intersecting each other in P.
4. Join AP and extend to R.
5. From AR, cut off AD = H.
6. With centre B and any radius, draw an arc intersecting AB in G and H.
7. With centres G and H and the same radius, draw arcs on the same side of AB, intersecting each other in Q.
8. Join BQ and extend to S.
9. From AS, cut off BC = h.
10. Join DC and extend it both sides.
Thus, DC is the required line which is parallel to AB and is at a distance of H from AB.
Construction: To construct a line parallel to a given line, through a point outside the line.
Steps of Construction:
1. Take any point Q on xv.
2. Join PQ.
3. Construct a ray PR, with R on the side of PQ, opposite to Y such that ?QPR = ?PQY
4. Produce ray PR to line PR.
Line RP is the required line parallel to XY
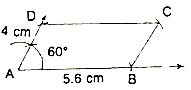
Construction: To construct a parallelogram when two consecutive sides and the included angle are given.
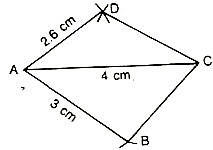
Construction: To construct a parallelogram when its two consecutive sides and a diagonal are given.
Live Math Experts: Help with Construction Assignments - Homework
Expertsmind.com offers help with Construction assignment and homework in mathematics subject. Experts mind’s math experts are highly qualified and experienced and they can solve your complex Construction math problems within quick time. We offer email based assignment help –homework help service in all math topics including Construction .
Math Online Tutoring: Construction
We at Expertsmind.com arrange instant online tutoring session in Construction math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Construction Math topic and provide you tricky approach to solve complex Construction problems.