Straight lines - Angle between Two Straight Lines, Math

Angle between Two Straight Lines:

(1)     The angle a between two lines whose slopes are m, and m₂ is given by m₁-m₂

tan q =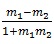 

If q is angle between two lines then p-q is also the angle between them.

If the value of tan a given by the above formula is positive we get the acute angle between the lines and if it is negative, we get the obtuse angle between the lines.

(i)      If the lines are parallel, then m₁ = m₂

(ii)     If the lines are perpendicular, then m₁m2 = - 1

(2)     If the given equation of straight lines are a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = q, then the angle between the lines q² is given by

 

tan q = a₁a₂ + b₁b₂

Note:

(i)      If the lines are parallel, then

 

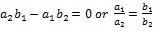
(ii)     If the lines are perpendicular, then a₁a₂ + b₁b₂ = 0.

(iii)    The slope of a line parallel to x-­axis is 0 as slope of x-axis is 0. (iv)    The slope of a line parallel to y-­axis is not defined.

(v)     The slope is independent of the sense of the line segment i.e., slope of AB = slope of BA.

 

The equation of any straight line: parallel to a given line ax + by + C = 0 is ax + by + k = 0.

The equation of any straight line perpendicular to a given line, ax + by + c = 0 is bx - ay + k = 0.

The equation of any straight line passing through the point of intersection of two given lines l1 = a₁x + b₁y + c = 0 and l_{2 =} a₂x + b₂y + c₂ = 0 is

 

l2 + Al2 = 0

Where A is any real number, which can be determined by given additional condition in the question.

The length of perpendicular from a given point (x₁, v₁) to a given line ax + by + c = 0 is

          

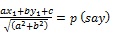
          In particular, the length of perpendicular from origin (0, 0) to the line

ax + by + c = 0 is 

 

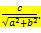
Position of Two Points with respect to a line: Two points (x₁, y₁) and (x₂, y₂) are on the same side or on the opposite side of the straight line ax + by + c = 0 according as the values of ax₁ + by₁ + c and ax₂ + by₂ + c are of the same sign or of opposite sign.

 

Equations of Bisectors: The equations of bisectors of the angles between the lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂= 0 are

           

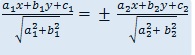
Note: Any point on a bisector is Equidistant from the given lines.

(i)      Equation of the bisector of the angle in which the origin lies is

                                              

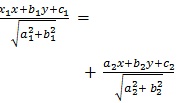
provided the equations of the lines are so written that c₁ and c₂ are either both positive or both negative.

 

(ii)     If e be angle between one of the given lines and one bisector, then if the absolute value of tan q i.e.,

| tan q| < 1, then it is the bisector of acute angle and if | tan q | > 1, then it is the bisector of obtuse angle.

 

(iii)    If the constant terms c₁ and c₂ and a₂x + b₂y + c₂ = 0 are of the same sign, then the angle between these two lines in which the origin lies is acute if a₁a₂ + b₁b₂ < 0 and obtuse if a₁a₂ + b₁b₂ > 0.

 

Live Math Experts: Help with Straight lines Assignments - Homework

Expertsmind.com offers help with Straight lines assignment and homework in mathematics subject. Experts mind’s mathexperts are highly qualified and experienced and they can solve your complex Straight lines math problems within quick time. We offer email based assignment help –homework help service in all math topics including Straight lines .

Math Online Tutoring: Straight lines - Co-ordinate Geometry

We at Expertsmind.com arrange instant online tutoring session in Straight lines math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Straight lines Math topic and provide you tricky approach to solve complex Straight lines problems.